Sådan udregner du standardafvigelse i Excel

Standardafvigelse (også kaldet spredning) bruges inden for sandsynlighedsregning.

Den fortæller noget om usikkerheden på ens data, da man kigger på hvor meget variation der er i dit datasæt. Altså hvor langt disse afviger fra middeltallet.

Standardafvigelsen kan beregnes på flere måder i Excel.

Du vil i denne artikel lære at bruge Excels funktioner, ud fra forskellige forudsætninger, til at estimere standardafvigelsen.

Indholdsfortegnelse

Download øvelsesfilen

Inden du går i gang med resten af guiden, så download øvelsesfilen og følg de trin jeg viser dig.

Afhængigt af dit datasæt, er der forskellige funktioner i Excel til at beregne standardafvigelsen.

Disse funktioner er relativt nye og erstatter den gamle STDAFV, som du måske kender fra de tidligere versioner af Excel.

Fordelen med de nye er, at du kan nå en mere nøjagtig standardafvigelse, da du kan vælge den funktion, som passer bedst til dit datasæt.

Valget af funktion afhænger af to parametre:

• Indeholder datasættet hele populationen eller en stikprøve (del af population)?
• Skal der medtages ’ulovlige’ værdier, såsom tekst, eller kun tal?

Dette giver dig fire forskellige funktioner; STDAFV.P, STDAFV.S, STDAFVPV og STDAFVV, som fordeler sig således:

Jeg vil nu gennemgå de forskellige funktioner – husk at downloade øvelsesfilen, så du selv kan prøve kræfter med det.

STDAFV.P og STDAFV.S bruges hvis dine data kun er tal, til at estimere standardafvigelsen – for enten en del eller hele populationen. Dette er dem du nok oftest vil bruge.

• STDAFV.P estimerer på basis af hele populationen.
• STDAFV.S estimerer på basis af stikprøver. Altså en del af populationen.

Du vælger således funktion efter hvad dine data repræsenterer, for at få beregnet så nøjagtig en standardafvigelse som muligt.

Deres lighed består i, at de kun accepterer tal og dermed ignorerer ‘ulovlige værdier’ såsom logiske værdier og tekst.

Som ved alle andre funktioner i Excel, har STDAFV.P og STDAFV.S en syntaks.

Syntaks dækker over, hvad du putter ind i funktionen for at få et resultat.

En syntaks består af forskellige argumenter, hvor disse to funktioner består af to Tal1 og Tal2

STDAFV.P(tal1;[tal2];…)

STDAFV.S(tal1;[tal2];…)

Tal1 er påkrævet repræsenterer det første talargumenter, som svarer til en stikprøve af populationen, hvorefter Tal2 (som er valgfrit) dækker over talargumenter fra 2 op til 254, fra stikprøven af populationen.

DOG Kan du også anvende en enkelt matrix (eller en reference til en matrix) i stedet for dine manuelle argumenter.

Dette gør jeg i de efterfølgende eksempler.

Sådan bruger du STDAFV.P

STDAFV.P beregner som bekendt standardafvigelsen baseret på hele populationen. Hvis datasættet i stedet repræsenterer en del (stikprøve) af populationen, skal STDAFV.S bruges til at beregne standardafvigelsen.

STDAFV.P’ syntaks ser således ud:

=STDAFV.P(tal1;[tal2];…)

I dette eksempel har vi et lille datasæt (matrix), som vi ønsker at finde standardafvigelsen på. Hvis vi indsætter funktionen, kan du blot markere dine data, her tal, som herefter udfylder din funktion med din matrix:

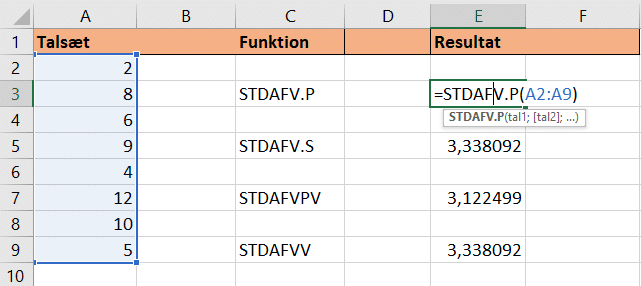
Når du har udfyldt syntaksen og trykket Enter, har du hermed standardafvigelsen for hele populationen.

Sådan bruger du STDAFV.S

STDAFV.S fungerer som STDAFV.P men forudsætter, modsat STDAFV.P, at argumenterne er en stikprøve/del af populationen.

STDAFV.S’ syntaks består af samme argumenter og ser således ud:

=STDAFV.S(tal1;[tal2];…)

Vi prøver nu at udregne standardafvigelsen på samme matrix, som ved STDAFV.P:

Når du har udfyldt syntaksen og trykket Enter, har du hermed standardafvigelsen for en stikprøve/ del af populationen.

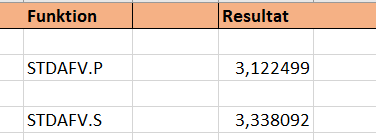
Hermed ser vi nu to forskellige standardafvigelser, der hver især tager højde for to forskellige usikkerheder, afhængigt af om der er tale om en stikprøve eller en hel population.

Funktionerne STDAFVPV og STDAFVV fungerer som de to andre funktioner – så længe der kun er talværdier i dine datasæt!

Således dækker disse funktioner også over stikprøver og hele populationer:

• STDAFVPV estimerer på basis af hele populationen.
• STDAFVV estimerer på basis af stikprøver. Altså en del af populationen.

Hvis dit datasæt indeholder andet end tal, f.eks. logiske værdier og tekstgengivelser af tal såsom ‘to’, vil disse funktioner kunne medtage disse i udregningen af standardafvigelsen.

Disse funktioner kan således være nyttige hvis du eksempelvis har indsamlet spørgeskemaer hvor nogle af dine respondenter ikke har svaret med tal, men med tekst.

DOG vil argumenter der er fejlværdier, eller tekst, som ikke kan oversættes til tal, forårsage fejl.

Funktionernes syntaks er næsten identisk med de to andre funktioners. Dog består forskellen i, at argumenterne her hedder ‘værdier’, da disse ikke kun accepterer tal:

STDAFVPV(værdi1;[værdi2];…)

STDAFVV(værdi1;[værdi2];…)

Udover accepten af de ellers ‘ulovlige’ værdier er funktionerne således identiske, hvorfor du også her kan benytte funktionerne på matrixer.

Hvis vi laver funktionerne på samme datasæt som før, bliver det ens resultater med tal:

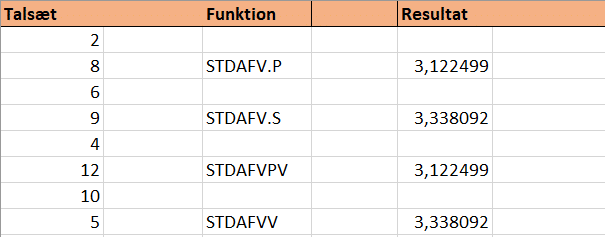
Derfor prøver vi med et nyt datasæt, som også indeholder tegn.

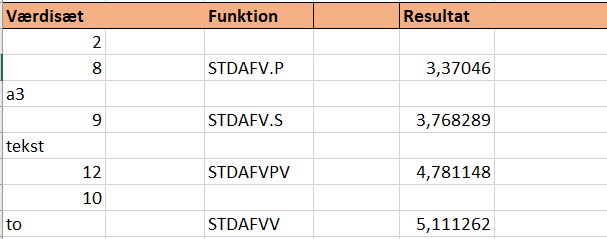
Trods samme datasæt får vi nu fire forskellige dataafvigelser.

De to sidste registrerer blandt andet ‘to’ som en tekstgengivelse af et tal, hvor både STDAFV.P og STDAFV.S ignorerer den værdi.

Synes du, at det gik lidt for stærkt, kan du nedenunder også se mine udregninger på STDAFVPV og STDAFVV:

Sådan bruger du STDAFVPV

Til at udregne standardafvigelsen for en hel population, hvor der også kan være andre værdier end tal, bruger vi følgende syntaks

=STDAFVPV(værdi1;[værdi2];…)

Til udregningen i det sidste eksempel, ser den således ud:

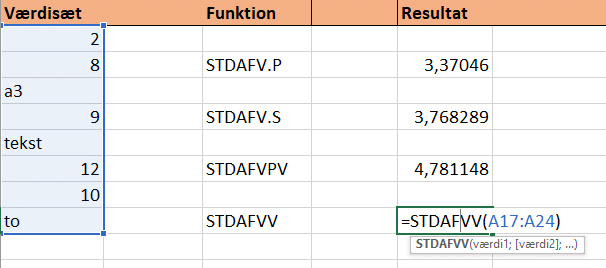
Sådan bruger du STDAFVV

Til at udregne standardafvigelsen for en stikprøve/del af en population, hvor der også kan være andre værdier end tal, bruger vi følgende syntaks

=STDAFVV(værdi1;[værdi2];…)

Til udregningen i det sidste eksempel, ser den således ud:

Du har nu lært at udregne standardafvigelser i Excel – og endda med mulighed for at gøre disse ekstra nøjagtige.

Du har nemlig lært fire forskellige funktioner, som tager højde for hvilke værdier du har til rådighed, men også om det er en stikprøve eller en hel population.

Stærkt! Du kan nu få nogle mere præcise data at arbejde med!

Lær mere!

Ønsker du at lære mere omkring redskaber til statistik?

Måske du kunne have brug for at lave et boksplot til sammenligning af populationer?